Page 56 - 国外钢铁技术信息内参（2024年9月）

ᇏݓࣁඋ࿐߶

ᇏݓࣁඋ࿐߶

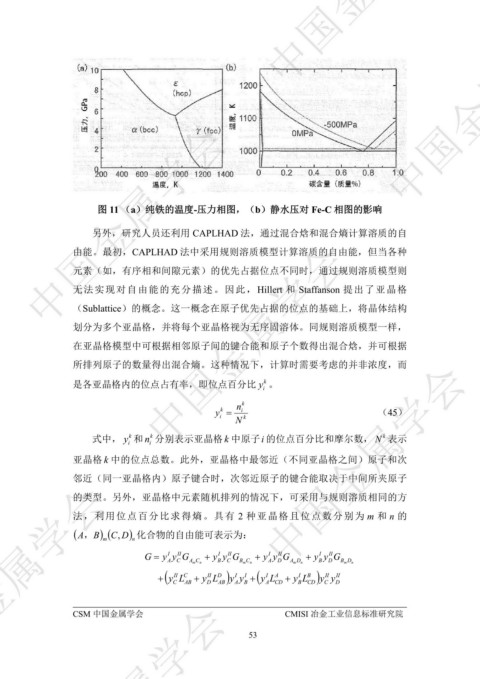
图 11 （a）纯铁的温度-压力相图，（b）静水压对 Fe-C 相图的影响 ᇏݓࣁඋ࿐߶

另外，研究人员还利用 CAPLHAD 法，通过混合焓和混合熵计算溶质的自 ᇏݓࣁඋ࿐߶
ᇏݓࣁඋ࿐߶
由能。最初，CAPLHAD 法中采用规则溶质模型计算溶质的自由能，但当各种

元素（如，有序相和间隙元素）的优先占据位点不同时，通过规则溶质模型则

无法实现对自由能的充分描述。因此，Hillert 和 Staffanson 提出了亚晶格

（Sublattice）的概念。这一概念在原子优先占据的位点的基础上，将晶体结构

划分为多个亚晶格，并将每个亚晶格视为无序固溶体。同规则溶质模型一样，

在亚晶格模型中可根据相邻原子间的键合能和原子个数得出混合焓，并可根据
ᇏݓࣁඋ࿐߶
ᇏݓࣁඋ࿐߶
所排列原子的数量得出混合熵。这种情况下，计算时需要考虑的并非浓度，而
k
是各亚晶格内的位点占有率，即位点百分比 y 。
i
n k
y  i （45）
k
i
N k
k
k
k
式中， y 和 n 分别表示亚晶格 k 中原子i 的位点百分比和摩尔数， N 表示
i
i
亚晶格 k 中的位点总数。此外，亚晶格中最邻近（不同亚晶格之间）原子和次
邻近（同一亚晶格内）原子键合时，次邻近原子的键合能取决于中间所夹原子
ᇏݓࣁඋ࿐߶
的类型。另外，亚晶格中元素随机排列的情况下，可采用与规则溶质相同的方

法，利用位点百分比求得熵。具有 2 种亚晶格且位点数分别为 m 和 n 的

A， B  C, D  化合物的自由能可表示为：
m
n
G  y I A y C II G A m C n  y I B y C II G B m C n  y I A y D II G A m D n  y B I y D II G B m D n

 y C II L  y D L D  yy I A I B   Ly I A A CD  y I B L B y C II y D
C
II
II
CD
AB
AB
ᇏݓࣁඋ࿐߶
CSM 中国金属学会 CMISI 冶金工业信息标准研究院
53