Page 10 - 国外钢铁技术信息内参（2024年12月）

ᇏݓࣁඋ࿐߶

垒，克服这种势垒的应力称为非热应力（ ），该应力不受温度影响，通常产
i
生于晶界和夹杂物等较大第二相中。 ᇏݓࣁඋ࿐߶

ᇏݓࣁඋ࿐߶

ᇏݓࣁඋ࿐߶

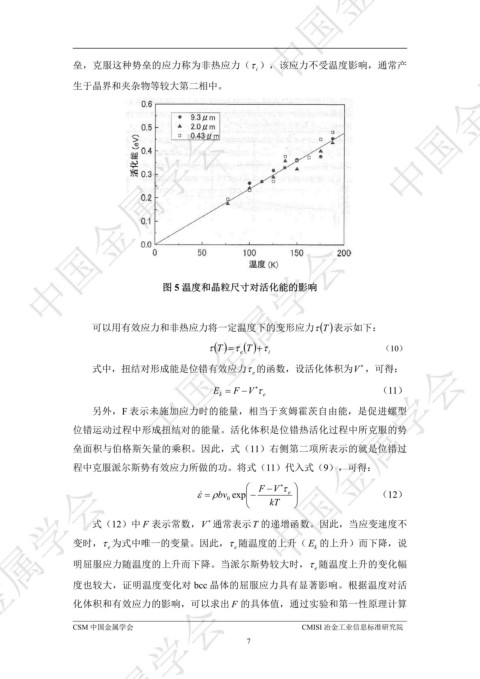
图 5 温度和晶粒尺寸对活化能的影响 ᇏݓࣁඋ࿐߶

T

可以用有效应力和非热应力将一定温度下的变形应力  表示如下：
T
T
    e    i （10）
ᇏݓࣁඋ࿐߶
ᇏݓࣁඋ࿐߶

式中，扭结对形成能是位错有效应力 的函数，设活化体积为V ，可得：
e

E  F  V  e （11）
k
另外，F 表示未施加应力时的能量，相当于亥姆霍茨自由能，是促进螺型
位错运动过程中形成扭结对的能量。活化体积是位错热活化过程中所克服的势

垒面积与伯格斯矢量的乘积。因此，式（11）右侧第二项所表示的就是位错过

程中克服派尔斯势有效应力所做的功。将式（11）代入式（9），可得：
ᇏݓࣁඋ࿐߶

 F V  
   bv 0 exp  e   （12）

 kT 

式（12）中 F 表示常数，V 通常表示T 的递增函数。因此，当应变速度不

变时， 为式中唯一的变量。因此， 随温度的上升（ E 的上升）而下降，说
k
e
e
明屈服应力随温度的上升而下降。当派尔斯势较大时， 随温度上升的变化幅
e
度也较大，证明温度变化对 bcc 晶体的屈服应力具有显著影响。根据温度对活

ᇏݓࣁඋ࿐߶
化体积和有效应力的影响，可以求出 F 的具体值，通过实验和第一性原理计算

CSM 中国金属学会 CMISI 冶金工业信息标准研究院
7