Page 49 - 国外钢铁技术信息内参（2024年9月）

ᇏݓࣁඋ࿐߶

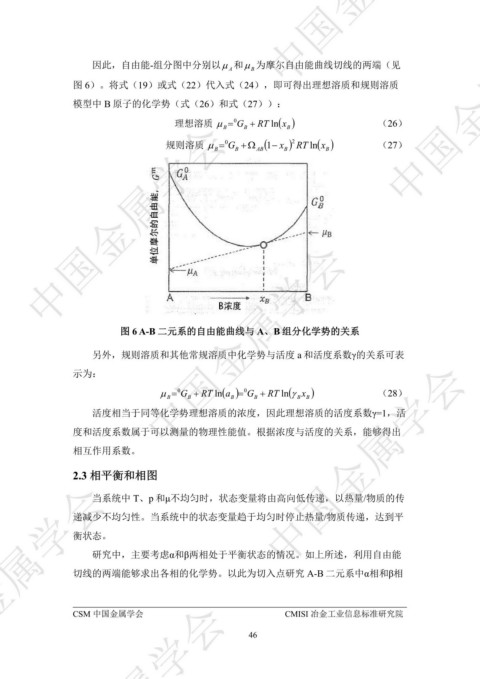
因此，自由能-组分图中分别以  和  为摩尔自由能曲线切线的两端（见
A
B
图 6）。将式（19）或式（22）代入式（24），即可得出理想溶质和规则溶质

模型中 B 原子的化学势（式（26）和式（27））： ᇏݓࣁඋ࿐߶

x
理想溶质  B  0 G  RT ln   （26）
ᇏݓࣁඋ࿐߶
B
B
2
规则溶质  B  0 G   AB 1 x B  RT ln   （27） ᇏݓࣁඋ࿐߶
x
B
B

ᇏݓࣁඋ࿐߶

图 6 A-B 二元系的自由能曲线与 A、B 组分化学势的关系

另外，规则溶质和其他常规溶质中化学势与活度 a 和活度系数γ的关系可表
ᇏݓࣁඋ࿐߶
示为：

  0 G  RT ln   Ga  0 B  RT ln  x B B  （28）
B
B
B
活度相当于同等化学势理想溶质的浓度，因此理想溶质的活度系数γ=1，活
度和活度系数属于可以测量的物理性能值。根据浓度与活度的关系，能够得出

相互作用系数。 ᇏݓࣁඋ࿐߶

2.3 相平衡和相图
ᇏݓࣁඋ࿐߶
当系统中 T、p 和μ不均匀时，状态变量将由高向低传递，以热量/物质的传

递减少不均匀性。当系统中的状态变量趋于均匀时停止热量/物质传递，达到平

衡状态。

研究中，主要考虑α和β两相处于平衡状态的情况。如上所述，利用自由能

切线的两端能够求出各相的化学势。以此为切入点研究 A-B 二元系中α相和β相

ᇏݓࣁඋ࿐߶
CSM 中国金属学会 CMISI 冶金工业信息标准研究院

46