Page 56 - 国外钢铁技术信息内参(2025年1月)
P. 56
包含多个溶质原子Y用 Labusch极限表达更加合适 这种情况下Y固溶强化量
与溶质浓度的 2/3次方成正比
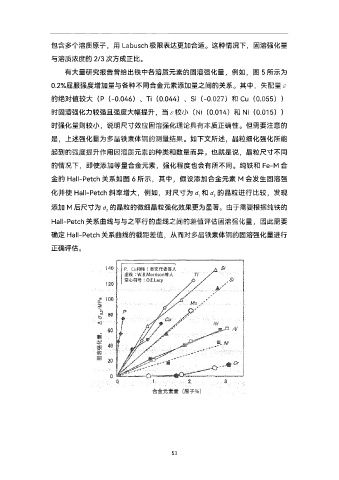
有大量研究报告曾给出铁中各溶质元素的固溶强化量Y例如Y图 5所示为
0.2%屈服强度增加量与各种不同合金元素添加量之间的关系 其中Y失配量
的绝对值较大½P½-0.046¾ Ti½0.044¾ Si½-0.027¾和 Cu½0.055¾¾
时固溶强化力较强且强度大幅提升Y当 较小½Ni½0.014¾和 Ni½0.015¾¾
时强化量则较小Y说明尺寸效应固溶强化理论具有本质正确性 但需要注意的
是Y上述强化量为多晶铁素体钢的测量结果 如下文所述Y晶粒细化强化所能
起到的强度提升作用因溶质元素的种类和数量而异 也就是说Y晶粒尺寸不同
的情况下Y即使添加等量合金元素Y强化程度也会有所不同 纯铁和 Fe-M合
金的 Hall-Petch关系如图 6所示Y其中Y假设添加合金元素 M会发生固溶强
化并使 Hall-Petch斜率增大Y例如Y对尺寸为 d 和 d 的晶粒进行比较Y发现
1 2
添加 M后尺寸为 d 的晶粒的微细晶粒强化效果更为显著 由于需要根据纯铁的
2
Hall-Petch关系曲线与与之平行的虚线之间的差值评估固溶强化量Y因此需要
确定 Hall-Petch关系曲线的截距差值Y从而对多晶铁素体钢的固溶强化量进行
正确评估
53